El Mundo Divertido De Las Matemáticas, Las Ciencias S y N: 2013

Operaciones de Números Enteros

http://www.youtube.com/watch?v=Sj9rThGLz9Q

Regla de los signos
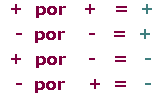
signos

Suma

En la suma de dos números enteros, se determina por separado el signo y el valor absoluto del resultado.

Para sumar dos números enteros, se determina el signo y el valor absoluto del resultado del siguiente modo:

Si ambos sumandos tienen el mismo signo: ese es también el signo del resultado, y su valor absoluto es la suma de los valores absolutos de los sumandos.

Si ambos sumandos tienen distinto signo:

El signo del resultado es el signo del sumando con mayor valor absoluto.

El valor absoluto del resultado es la diferencia entre el mayor valor absoluto y el menor valor absoluto, de entre los dos sumandos.

Ejemplo. (+21) + (−13) = +8 , (+17) + (+26) = +43 , (−41) + (+19) = −22 , (−33) + (−28) = −61
La suma de números enteros se comporta de manera similar a la suma de números naturales:

La suma de números enteros cumple las siguientes propiedades:

Propiedad asociativa. Dados tres números enteros a, b y c, las sumas (a + b) + c y a + (b + c) son iguales.

Propiedad conmutativa. Dados dos números enteros a y b, las sumas a + b y b + a son iguales.

Elemento neutro. Todos los números enteros a quedan inalterados al sumarles 0: a + 0 = a.

Ejemplo.

Propiedad asociativa:
[ (−13) + (+25) ] + (+32) = (+12) + (+32) = (+44)
(−13) + [ (+25) + (+32) ] = (−13) + (+57) = (+44)
Propiedad conmutativa:
(+9) + (−17) = −8
(−17) + (+9) = −8

Además, la suma de números enteros posee una propiedad adicional que no tienen los números naturales:

Elemento opuesto o simétrico. Para cada número entero a, existe otro entero −a, que sumado al primero resulta en cero: a + (−a) = 0.

Resta

La resta de números enteros es muy sencilla, ya que ahora es un caso particular de la suma.

La resta de dos números enteros (minuendo menos sustraendo) se realiza sumando el minuendo más el sustraendo cambiado de signo.

Ejemplos
(+10) − (−5) = (+10) + (+5) = +15
(−7) − (+6) = (−7) + (−6) = −13
(−4) − (−8) = (−4) + (+8) = +4
(+2) − (+9) = (+2) + (−9) = −7
Estrictamente, si a y b son dos enteros cualesquiera entonces

a - b = a + (-b), donde se entiende que (-b) es el opuesto o simétrico de b, que siempre existe. Ese hecho asegura que la sustracción de enteros sea una operación binaria en ℤ

Multiplicación

La multiplicación de números enteros, al igual que la suma, requiere determinar por separado el signo y valor absoluto del resultado.

En la multiplicación (o división) de dos números enteros se determinan el valor absoluto y el signo del resultado de la siguiente manera:

El valor absoluto es el producto de los valores absolutos de los factores.

El signo es «+» si los signos de los factores son iguales, y «−» si son distintos.

Para recordar el signo del resultado, también se utiliza la regla de los signos:

Regla de los signos

(+) × (+)=(+) Más por más igual a más.

(+) × (−)=(−) Más por menos igual a menos.

(−) × (+)=(−) Menos por más igual a menos.

(−) × (−)=(+) Menos por menos igual a más.

Ejemplo. (+4) × (−6) = −24 , (+5) × (+3) = +15 , (−7) × (+8) = −56 , (−9) × (−2) = +18.
La multiplicación de números enteros tiene también propiedades similares a la de números naturales:

La multiplicación de números enteros cumple las siguientes propiedades:

Propiedad asociativa. Dados tres números enteros a, b y c, los productos (a × b) × c y a × (b × c) son iguales.

Propiedad conmutativa. Dados dos números enteros a y b, los productos a × b y b × a son iguales.

Elemento neutro. Todos los números enteros a quedan inalterados al multiplicarlos por 1: a × 1 = a.

Ejemplo.

Propiedad asociativa:

[ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140
(−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140
Propiedad conmutativa:
(−6) × (+9) = −54
(+9) × (−6) = −54

La suma y multiplicación de números enteros están relacionadas, al igual que los números naturales, por la propiedad distributiva:

Propiedad distributiva. Dados tres números enteros a, b y c, el producto a × (b + c) y la suma de productos (a × b) + (a × c) son idénticos.

Ejemplo

(−7) × [ (−2) + (+5) ] = (−7) × (+3) = −21
[ (−7) × (−2) ] + [ (−7) × (+5) ] = (+14) + (−35) = −21

División de Números Enteros

La división es la operación inversa de la multiplicación.

Dividendo : divisor = cociente

divisor · cociente = Dividendo
Dividir es hallar el número por el que se debe multiplicar al divisor para obtener el dividendo.
En la división de números enteros se cumple la misma norma de signos que en la multiplicación.(+) : (+) = +
(+) : (-) = -
(-) : (+) = -
(-) : (-) = +
La división no es una operación interna en el conjunto de los números enteros.
Es decir, al dividir dos números enteros puede ser que no resulte otro número entero.
Además nunca se puede dividir por el número 0.

http://www.aaamatematicas.com/div65_x2.htm

NúmerosEnteros

El hombre desde siempre a tratado de buscar soluciones a sus necesidades, es por esto que utilizó su inteligencia para descubrir un mecanismo que le permitiera representar sus egresos e ingresos. Comenzó utilizando palitos rojo para simbolizar las perdidas y palitos negro para saber cuánto eran sus ganancias.

Al pasar del tiempo los palitos rojos pasaron a ser números negativos y los palitos negros números positivos dando lugar al Conjunto de Números Enteros. Es así como se amplía el Conjunto de Números Naturales (Ν), considerando los naturales y sus opuestos.

Para representar los números enteros se utiliza la letra Ζ. Este conjunto numérico está formado por los números enteros negativos, el cero y los números enteros positivos.

El siguiente diagrama nos expresa todo lo anterior: